How Do You Measure Volume Of A Gas

The relationship between the amounts of products and reactants in a chemical reaction can be expressed in units of moles or masses of pure substances, of volumes of solutions, or of volumes of gaseous substances. The ideal gas law can be used to calculate the volume of gaseous products or reactants as needed. A gas collected in such a way is not pure, however, but contains a significant amount of water vapor. The measured pressure must therefore be corrected for the vapor pressure of water, which depends strongly on the temperature.

Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law).

The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). The ideal gas law specifies that the volume occupied by a gas depends upon the amount of substance as well as temperature and pressure. Standard temperature and pressure -- usually abbreviated by the acronym STP -- are 0 degrees Celsius and 1 atmosphere of pressure. Parameters of gases important for many calculations in chemistry and physics are usually calculated at STP.

An example would be to calculate the volume that 56 g of nitrogen gas occupies. Measuring the volume of a bubble, especially at its detachment, is a basic subject in gas-liquid two-phase flow research. A new indirect method for this measurement under constant flow conditions is presented. An electronic device is designed and constructed based on laser beam intensity. This device calculates the frequency of the bubble formation by measuring the total time of the formation process and counting the number of bubbles crossing the laser beam. The bubble volume at detachment can be calculated by dividing the volumetric flow rate of air by the frequency of bubble formation.

The latter and the bubble volume at detachment are measured for three different heights of water above the the tip of the orifice , three orifice diameters , and different gas flow rates between 2000 and ml/hr. Comparing and validating the results with the results of the image processing method and the correlations presented by other studies shows the strong accuracy of the present method. Because the gas is less dense than liquid water, it bubbles to the top of the bottle, displacing the water.

Eventually, all the water is forced out and the bottle contains only gas. This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in .

An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11. Measurement of gas volume would be in either cubic meters or cubic feet gas units. When it is not under pressure, LPG exists in its gaseous or vapour form.

As with other gases, the gas measurement unit for volume of LPG is measured in cubic meters . Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter.

Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures. Estimation of headspace gas volume from headspace pressure in in vitro batch culture experiments conducted in our laboratory is currently done using equations derived from studies conducted overseas.

Consequently, the analytical capacity of the batch culture system is enhanced (Mauricio et al. 1999). The adoption of a predictive equation assumes a very small variation in the bottle headspace volume and atmospheric pressure ; however, these factors can greatly differ among laboratories. In addition, heat loss from bottles at the time of pressure reading can also vary depending on each laboratory setup, although it is assumed to be unaltered (Mauricio et al. 1999). Thus, the objective of the present work was to generate an equation to estimate GV from GP based on data obtained under our own laboratory conditions. Such an equation would be beneficial to others as it could be used to estimate GV in further experiments conducted using the batch culture system under similar experimental conditions. To distinguish actual volumetric flow rate from standardized volumetric flow rate, we commonly preface each unit with a letter "A" or letter "S" as the case may be e.g.

Here, ACFM means actual cubic foot per minute which is the volume of the gas at the flowing conditions. SCFM means standard cubic foot per minute which is the volume of the same gas now at standard conditions of temperature and pressure. The volume of carbon dioxide gas produced can be measured using a gas syringe. Using a measuring cylinder, add 50 cm3 of dilute hydrochloric acid to a conical flask. Immediately connect the gas syringe and start a stop clock. At times you may be required to record the volumetric flow rate of gases.

This can be achieved by making use of commercially available gas flow meters. The flow rates can be converted to the flow volumes by recording the temperature and pressure. A method based on body plethysmography for the assessment of thoracic gas volume in the anesthetized, paralyzed subject is presented. The compression of thoracic gas following inflation is detected by measuring the difference between the inflation volume and the "box volume" change caused by the expansion of the chest.

Model experiments showed good agreement between true and measured volumes with a residual standard deviation of 2 per cent. In studies on human subjects with healthy lungs during halothane anesthesia, the coefficient of variation of repeated measurements was 5 per cent. This difference, amounting to 0.2 liters on the average, may be explained by abdominal gas and by the detection of trapped gas by the box technique but not by the nitrogen washout.

The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. Many chemistry and physics experiments involve collecting the gas produced by a chemical reaction and measuring its volume.

Water displacement represents one of the easier methods to accomplish this task. The technique typically involves filling a glass column open on one end with water and then inverting the column and submerging the open end in a bowl of water. Columns built specifically for this purpose are called eudiometer tubes. The determined volume of a gas becomes useful only if the pressure of the gas is also known. This requires equilibration of the pressure inside the tube with atmospheric pressure. This resulted in the formulation of the laws of gases described in the next section 4a.

Along with how to use them in calculations and problem solving. On this blog, we have discussed in the past various flow meter technologies where a volumetric flow rate is required. It is also important that we discuss the unit of flow measurement in some of these flow meter technologies. This post intends to increase your understanding of volumetric flow rates in liquid and especially gas flow measurements. The specific volume, an intensive property, is the system's volume per unit of mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature.

For example, volume is related to the pressure and temperature of an ideal gas by the ideal gas law. As the gas is created, it will displace water from the bottle. The volume of gas can be determined by the amount of water that was displaced by the gas. The volume of gas collected and the gas laws can be used to calculate the number of moles of gas collected. The interest stems from that accurate measurements of the unit cell volume, atomic weight and mass density of a pure crystalline solid provide a direct determination of the Avogadro constant.

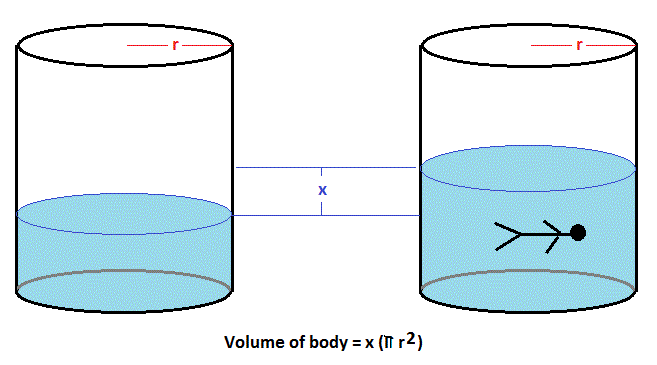
Measuring the volume depends on your object's state of matter. For liquids, you can use a graduated cylinder or burette for the chemistry lab measurements, or a measuring cup & spoon for everyday life purposes. For gases, to roughly measure the volume, you can inflate a balloon and use it to displace the water in a graduate cylinder.

A similar method works for solids — put the object into a graduated container and measure the change in reading. The volume of gas produced during a chemical reaction can be measured by collecting the gas in an inverted container filled with water. The gas forces water out of the container, and the volume of liquid displaced is a measure of the volume of gas. The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises. Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure.

The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales. To use the above formula, pressure and temperature must be in absolute units as envisaged by the ideal gas law. This makes volumetric flow measurement more tricky and complex for gases and vapours than for liquids.

One cubic meter of gas at high a pressure and temperature inside a process vessel will not occupy one cubic meter under different pressure and temperature conditions in the same vessel. This implies that volumetric flow measurement for gas is virtually meaningless without the accompanying data on pressure and temperature. If we need to work out the volume of a gas at other temperatures and pressures, we need to use the ideal gas equation. Real gases may not follow these rules precisely, but the volumes we work out are usually accurate enough for "A" level Chemistry.

Use common sense to calculate the volume of quantities of gas other than one mole. Clearly two moles of gas would occupy 48 dm3, that is 2 × 24. So, in general, multiply the number of moles by 24 to get the volume of gas in dm3 at room temperature and pressure. Natural gas is measured in volume at the resource well. One cubic foot of natural gas is the volume of gas contained in 1 cubic foot, at standard temperature and pressure.

Generally, the gas production measured from the reserves ranges in thousands or millions of cubic feet. Measurement of gas volume contributes to studies on reaction rates and commercial viability of chemical and biochemical processes in which a gas Is a by-product. Additionally measurement of volumes of vapours are also required for determination of molecular weights of volatile liquids by Victor – Meyer method.

To understand how the ideal gas equation and the stoichiometry of a reaction can be used to calculate the volume of gas produced or consumed in a reaction. A student was investigating the speed of reaction between limestone granules and different concentrations of hydrochloric acid. However after doing a whole series of experiments at different acid concentrations, there was no time to do the last planned experiment. The volume of carbon dioxide collected after 5 minutes in a 100cm3 gas syringe was used to determine the rate of reaction.

All the experiments were done in one lesson at a temperature of 22oC except for the last one. This was done in the next lesson, giving a carbon dioxide volume of 47.0 cm3 after 5 minutes, but at a higher temperature of 27oC . Gas volumemeans the volume of carbon dioxide gas, expressed at standard conditions dissolved in an equal volume of liquid. When a given volume of carbon dioxide gas, expressed at these standard conditions, is dissolved in the same volume of liquid, that liquid is said to have "one volume" of carbonation. The volume of dissolved carbon dioxide may be increased by lowering the liquid temperature and/or increasing the pressure of the gas.

This relationship shows us that the only way to increase the volume of gas, V, while maintaining the same temperature and pressure, is to increase the moles of gas, n, that are present, that is, add more gas. This relationship shows us that if we increase the moles of gas, n, by adding more gas while maintaining the same temperature and pressure, the volume of gas, V, will also increase. Gas measurement units are cubic metres, cubic feet, British Thermal Units , therms, and PSI as well as litres, kilograms, megajoules , tonnes and kilopascals for gas measurement.

The LPG gas is measured by weight in kilograms, pounds, tons or metric tonnes as gas measurement unit. … Standard temperature and pressure is defined as 0oC (273.15K) and 1atm pressure. The molar volume of a gas is the volume of one mole of a gas at STP. At STP, one mole (6.02×1023 representative particles) of any gas occupies a volume of 22.4L . Lower the eudiometer into the water-filled graduated cylinder prepared in step 1 until the water level inside the eudiometer tube is exactly even with the water level in the graduated cylinder.

At this point, the pressure inside the eudiometer tube is equal to the pressure outside the tube, i.e., atmospheric pressure. Now read the volume of the water level in the eudiometer tube. Because glassware manufacturers label the volume readings on eudiometer tubes from closed end to open end, this volume reading will reflect the volume of gas in the tube. The method by Raja Swaidan worked great for my system.

I just used a 100ml stainless steel with a know pressure (80-40psi). The change in pressure on connecting to the unknown volume gas line gave consistent values. I cross checked it by connecting to another stainless steel vessel of known volume instead of my gas line. It gave the exact volume of the second stainless steel vessel. The volume measured by this method was higher than the water method by about 15ml.

Also as I mentioned earlier there are numerous up and down bends in my line with rapid changes in tube diameter as well. I guest the bends and the changes in diameter are the reason for the inaccuracy in the water method. Measurement of volumes of liquids in comparison is simpler as a liquid can be measured using a graduated cylinder, a volumetric flask, burette, pipette or a graduated vial. This is possible because liquids acquire the shape of the measuring vessel and the meniscus level can be noted accurately without difficulty.